�V�E����앗�y�L
�R�c�����t���̎Z�z�`�p���[�X�|�b�g
 ��t���̎Z�z
��t���̎Z�z
�@�R�c����̖�t���̒��ɏオ�点�Ă��������A��t�@���l�Ɏ�������Ă���i�V��i�����Ă傤�j�����ƁA�Ԃ��O�p�`�̕`���ꂽ�̈���i�i�ԁj���ڂɓ���܂��B
����͋ߍ݂̘a�Z�Ƃ����w�̓�₪���������Ƃ�_���Ɋ��ӂ���ƂƂ��ɂ��̖����L���l�X�ɒm�点�邽�߂ɕ�[�����w�Z�z�x�ŁA�v�ۂ̏��R�������w��R�j�k�xNo.12�̒��Łu���̓��̎Z�z�̓��e�͗͊w�ł���A���������e�ł���B�v�ƏЉ�Ă��܂��B
�@�܂��{��s�̘a�Z�����ƁE�k���M���͕���29�N8���ɊJ�Â��ꂽ�{��s��������w��2����J�K�C�u���u�{��Ƃ��̎��ӂ̘a�Z�̗��j�Ɩ��͂ɂ��āv�Řa�Z�̍u�����s���A�{��s���ɂ���2�ʂ̎Z�z�Ƌ��ɎR�c�����t���́w�Z�z�x���Љ�Ă��܂��B
�����ŁA���w���ɂ�������悤�ȕ��@�Řa�Z�̖�肪������ΐ�l�̊����������ł����킦��̂ł͂Ǝv�������A���s���낵�Ȃ���g���C���Ă݂܂����B
�����y�Z�z�z
�@�a�Z�Ƃ������̔����������w�̖����@�������Đ_�ЂȂǂɕ�[�����G�n�B�z�ʑ�B�y�L�����z
�킳��y�a�Z�z
�@���{�×��̐��w�B�]�ˎ���Ɋ֍F�a���̑��̏r�˂݁A�������_�ɑ���������́A�~�����A�Ȑ��}�`�̖ʐς�ȖʂɈ͂܂ꂽ���̂̑̐ς����߂邱�ƂȂǂɓƎ��̔��B�����������A�����ɂȂ��ėA�����ꂽ���m���w�Ɉ��|���ꂽ�B �a�Z�̖��̂́A���̍��ɗm�Z�ɑ��č��ꂽ���́B�y�L�����z
��t���̎Z�z
 ��t���̊i�V��
��t���̊i�V��
����ǂ݉���
���������ɂ͂ǂ�ȓ��e�Ȃ̂���������K�v������̂ŁA�܂��܂��Ɓw�Z�z�x�߂Ă݂܂����B
�@�Ƃ��낪�`����Ă���̂͐Ԃ��O�p�`�Ɗ��������ŁA�������a�Z�̊w�p�p�ꂪ�܂܂�Ă��āA�����ƕ����Ă���łȂ��Ɠ��e�𐳂����c���ł������ɂȂ����Ƃ�������A�����Ȃ肨��グ�ł��B
�@���̂��ߎ��͂̓ǂ݉����͂���������߁A�}���ق֍s���Ē��쌧���̎Z�z�Ɋւ����发��T���o���A�a�Z�����҂ɂ���������Ė��̈Ӗ��m�ɂ���ƂƂ��ɁA��@���l����Q�l�ɂ��܂����B
�Z�z�̉��
�����M��E���쌧�a�Z�������̉�������p���܂��B
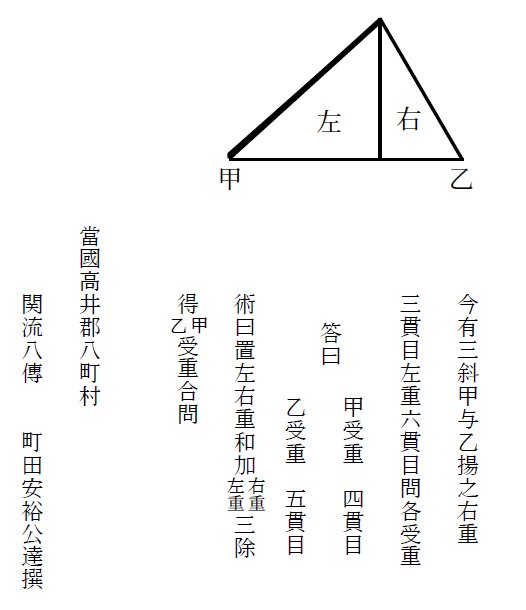 �R�c�����t��
�R�c�����t��
�m��[�n�i����j�������N�i1868�N�j
�m��[�҂Ƃ��̌n���n
�@��[�҂́A�z�ʂ�
�@�@�@�c������S�������@�֗����B���c���S���B��
�Ƃ���B�������͌��݂̌��݂̐{��s�����ł���B
���c�́A�R�c�����t����z��4�N�O�̌������N�i1864�N�j�ɐ{��s�i�����̊i�V��ɂ��Z�z���[���Ă���B
���̊z�ʂɂ�
�@�@�@�֗��������B�@�y��������l�@�����W�@���c���S���B��
�Ƃ���A�����̊z�ʂɁu�֗��������B�v�u�֗����B�v�Ɩ�����Ă��邪�A���c�̎t���͒N���s���ł���B
�m��n
�y��Ӂz�@�}�̂悤�ɁA�ώ��ȎO�i��ʎO�p�`�j�̔�����B
�E�̎O�p�`�̏d����3�іځA���̎O�p�`�̏d����6�іڂł���B�b�Ɖ��������グ��B
�@���̂Ƃ��̍b�A���̎�d�����߂�B
�y���z�@�b�̎�d�F4�іځA�@���̎�d�F5�і�
�y�p�z�@�b�̎�d���o�i���d�{�E�d�j�{�E�d�p/3
�@�@�@�@���̎�d���o�i���d�{�E�d�j�{���d�p/3
�����M��y���� ���Ⓑ�쌧�̎Z�z�z���
���c���S���B�ɂ���
�����M��̉���̂ق��ɂ����c���S���B�Ɋւ�������܂����B
�u���̓��̎Z�z�̓��e�͗͊w�ł���A���������e�ł���B��[�҂͍���S�������֗����`���c���S���B�ŁA���c�͈����ƌ����A�V��2�N�i1831�N�j�A���c���g�̓�j�Ƃ��Đ��܂�Ă���B�y���C����l�Ƃ���̂ŏ�Ւ��̓y����֒ʂ��A�֗��̎Z�w���w�l�ł���B�v
���R���u�R�c����̖�t���ɂ��āv���
�u���R���R�c����̖�t���̊i�V��ɕ`���ꂽ��ʂ̎Z�z������B�����P�N�i1868�j�ɕ�[���ꂽ���̂ł��邪�A�o��Ғ��c���B�ɂ��Ă͐{��s�����̐l�ł��邱�ƈȊO�͉����킩��Ȃ��B�i�V��ɕ`����Ă���Ƃ����`���Ƃ����A�d�S�ɂ��Ă̖��Ƃ����A�M�Z�ł͑��ɗ���݂Ȃ��Z�z�ł���B�v
�ԉH��߁u�M�Z�̘a�Z�v���
�����M��ɂ���
���쌧���̒��w�Z�ɋΖ�����T��A50�N�ɂ킽���Ęa�Z�̌����𑱂��A�����̎��ЂɎc�邷�ׂĂ̎Z�z���������܂����B
�@���a30�N��ɍ��R���w�Z��3�N�ԋ��ڂ����A���̊Ԃɘa�Z�����ҁE�ԉH��߂Ɠ��s���ĎR�c�����t���̎Z�z�����A���a39�N�i1964�N�j�Ɂw���y�̎Z�z : ���k�M�n���x�i�o�Œn�F���R���A���ʔŁj���Ă��܂��B
�@�����F���a8�N�i1933�N�j���쌧�����s�o�g
�@�@�@�@���a29�N�i1954�N�j�M�B��w����w���C���A���a43�N�i1968�N�j�ʐ��w���w������
�@�@�@�@���쌧�����w�Z��40�N�Ζ��A����6�N�i1994�N�j����s���k��q���w�Z�Z����N�ސE
�@�@�@�@����23�N�i2011�N�j�u�M���܁v���
�@�@�@�@����31�N�i2019�N�j���S�A���N85��
�@��啪��F���쌧�W�̘a�Z�����̏N�W�Ƃ��̌���
�@�����w��F���{���w�j�w��A���쌧�a�Z������
�@��v�����F�w���쌧�̎Z�z�x�i�����j�A�w�����̈̑�Ȃ鐔�w�ҁx�i�����j�A�w�����ɍ炢���a�Z�̉� : �w�Z�@��[����]�x�Ɗ����V��x�A�������B

�������M�펁���ÂԐM�Z�����V���L���i2019�N4��10���j
�����@
�a�Z�����҂ɂ�錻���@�@���̂P
�����M��̒����ɋL�ڂ���Ă����@�ł��B
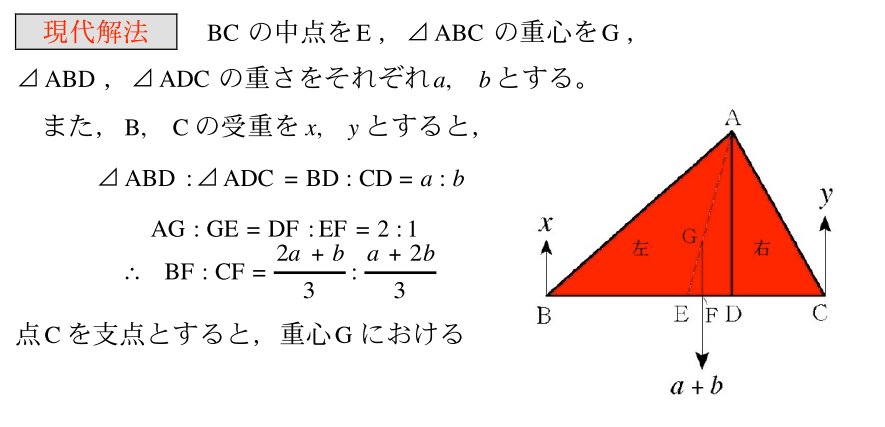

�y�p�Ƃ̊W�z�@�@�A�A�̎��́A�y�p�z�ɋL���ꂽ���ƈ�v����B
�����M��y���쌧�����Z�z�W�听�@�Z�z�ւ̏��ҁz���
�a�Z�����҂ɂ�錻���@�@���̂Q
�ԉH��߂̒����ɋL�ڂ���Ă����@�ł��B
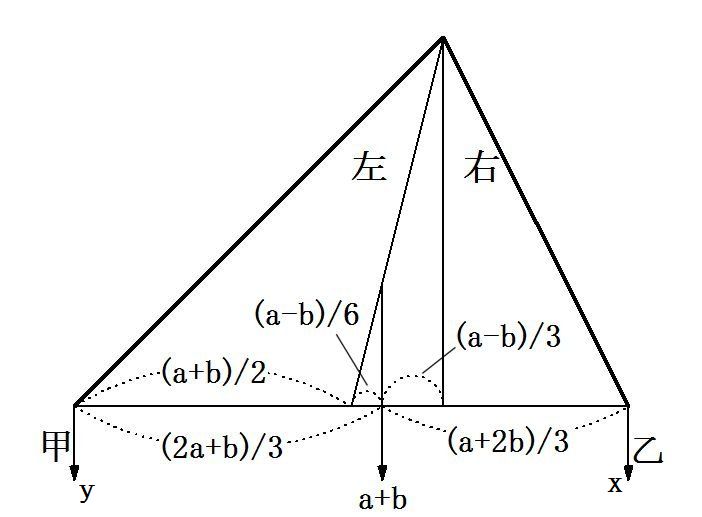
�@���E�̎O�p�`�̏d�������ꂼ�ꂁ�A���A�b���ɂ�����d�������A���Ƃ���B
�@�}����
�@�@�@�@�@(2a�{b)/3�~�ia�{b�j���ia�{b�jx
�@�@�@���@x��(2a�{b)/3��{(a�{b)�{a}/3
�@���l��
�@�@�@�@�@y=(a�{2b)/3={(a�{b)�{b}/3
�@�����ł����U�A�����R�Ƃ���Ɓ@�����T�A�����S
�@�@�@�@���@�b�̎�d�S�іځA���̎�d�T�і�
�ԉH��߁w�M�Z�̘a�Z�x���
���w���ɂ������������
�����M��̉���ɂ���ĎZ�z�ɏ�����Ă���y��z�Ɓy���z�̈Ӗ��͕�����܂������A�y�p�z�͐������Ȃ��̂łȂ�ł����Ȃ�̂��Ƃ��������s���ł��B
�@�܂������ƐԉH�ɂ�錻���@�����ƌ����ŁA�����ɔ[���ł���̂͐��w�̐搶�Ɨ��n�̍��Z���ȏ�Ɍ���ꂻ���Ȃ̂ŁA���w���ł��������蓚���o�������ȉ��������������܂��B
�������̃|�C���g
�����ƐԉH�̉������w�Z�z�x�́y��z�͒��w�Z�̐��w�Ɨ��Ȃ����킹���悤�Ȗ��ł��邱�Ƃ����������̂ŁA������������́i�P�j�h�O�p�`�̏d�S�h�Ɓi�Q�j�h�Ă��̌����h�i���[�����g�j���낤�Ɠ���������A�������̃|�C���g���܂Ƃ߂܂����B
�i�P�j�h�O�p�`�̏d�S�h�ɂ���
���イ����y�d�S�z
�@�k���l���̂̊e�����ɓ����d�͂̍��͂���p����ƍl������_�B���ʒ��S�B�d�͒��S�B
�@�k���l�O�p�`�ŁA�e���_�ƑΕӂ̒��_�Ƃ����Ԑ����̌�_�B�y�L�����z
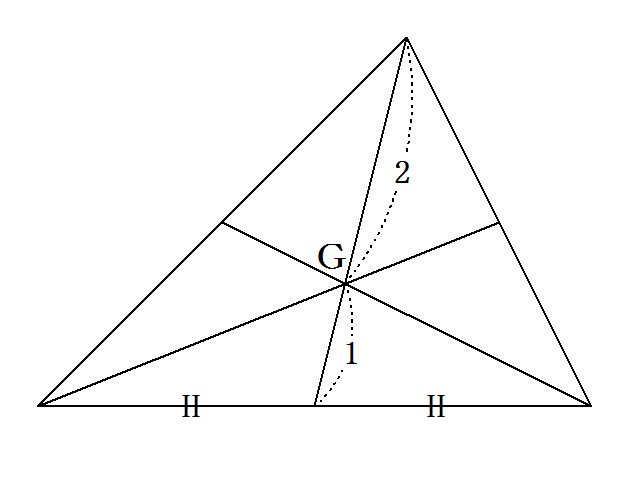 �@�܂��O�p�`�̏d�S�̐����Ƃ��Ď���3���ڂ�����܂��B
�@�܂��O�p�`�̏d�S�̐����Ƃ��Ď���3���ڂ�����܂��B
�@�@�P�j�O�p�`�̏d�S�͒����̌�_�ɂȂ�B
�@�@�Q�j�d�S�͒������Q�F�P�ɕ�����B
�@�@�R�j�R�{�̒����͏d�S�Ō����B
�i�Q�j�h�Ă��̌����h�ɂ���
�Ă��̂����y���q�̌����z
�@�_��1�_���x�_�Ƃ��A�����ȗ͂��x�_���牓���_�i�͓_�j�ɉ�����ƁA�x�_�ɋ߂��_�i��p�_�j�ő傫�ȗ͂�������Ƃ��������B �Ă����ނ荇���Ă���ƁA�͓_�A��p�_�ɂ������F�AW�ƁA�x�_���炱��2�_�܂ł̋���l�AL�̊ԂɁA Fl��WL �̊W������B�y�L�����z
���[�����g�ymoment�z
�@�k���l��ɉ�]�\�͂̑傫����\���ʁB��_����̈ʒu�x�N�g���ƒ��ڂ��镨���ʂƂ̃x�N�g���ςƂ��ĕ\�����B �͂̃��[�����g�A�^���ʂ̃��[�����g�i�p�^���ʁj�A�d�C�E���C�o�Ɏq���[�����g�ȂǁB�\���B�������g�B�y�L�����z
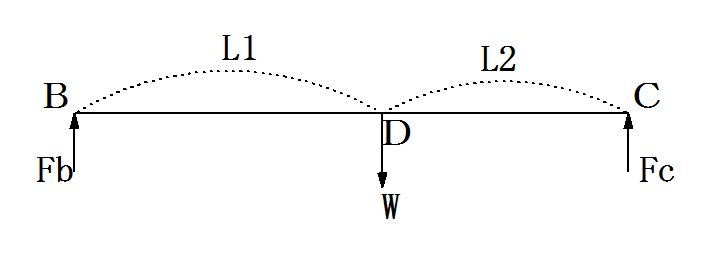
�@�}�ła�c�̒�����L1�A�c�b�̒�����L2�Ƃ��A�c�ɂ�����d���v�A�a�A�b�ɂ������d��Fb�AFc�A�Ƃ����
�@�@�@Fb�{Fc��W
�@�@�@W�~L1��Fc�~(L1�{L2)
�@�@�@W�~L2��Fb�~(L1�{L2)
�����藧�B���p�Ƃ��ĉd���Q�J���̏ꍇ�͈ȉ��̒ʂ�ɂȂ�B
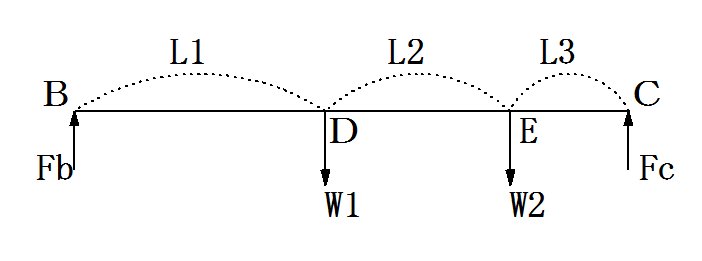
�@�@�@Fb�{Fc��W1�{W2
�@�@�@W1�~L1�{W2�~(L1�{L2)��Fc�~(L1�{L2�{L3)
�@�@�@W2�~L3�{W1�~(L3�{L2)��Fb�~(L1�{L2�{L3�j
���̐���
�����ɂ�錻���@�ɐ�����lj����Đ������܂��B
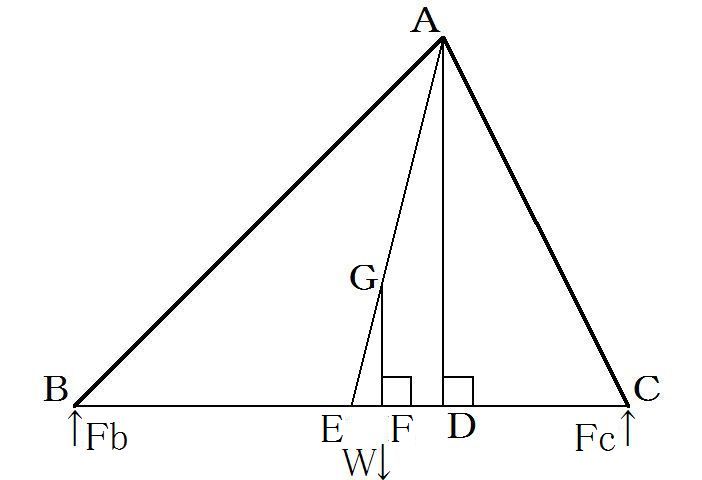 �}�P�@�d�S�Ɖd
�}�P�@�d�S�Ɖd
�m���n
�@�ގ����ψ�ȎO�p�`�̔� ��ABC ������A�d����W�ł���B
�@���_A�����BC�Ɉ����������ƕ�BC�Ƃ̌�_�i�����̑��j��D�Ƃ���B
�@���̂Ƃ���ABD �̏d����a�A��ACD �̏d����b�Ƃ���B���@W��a�{b
�@���_B��C�ŎO�p�`�̔��x����Ƃ��AB�̎�dFb��C�̎�dFc�����߂�B
�m�d�S�ƍ�p�_�n
�@�}�P�ɂ����ĕ�BC�̒��_��E�Ƃ��A���_A��E�����ԂƇ�ABC�̏d�S�͑O�q�i�P�j�̂P�j����AE��ɂ��邱�Ƃ�������B������
�@�@�@AG�FGE��2�F1
�ƕ�������_��G�Ƃ���ƁA�O�q�i�P�j�̂Q�j����G�͇�ABC�̏d�S�ɂȂ�B
�@�d�SG�����BC�ɉ��낵�������ƕ�BC�Ƃ̌�_�i�����̑��j��F�Ƃ���B
�@��ABC�̏d��W��F�ɏW������ƍl���邱�ƂŁAB��C�ɂ������d�́AB��C���x�_�Ɨ͓_�AF����p�_�Ƃ���"�Ă��̌���"�ŋ��߂邱�Ƃ��ł���B
�m�̏d���ƎO�p�`�̕ӂ̒����n
�@��ABD�̔̏d��a�A��ADC�̔̏d��b�ƁA���ꂼ��̎O�p�`�̒�ӂ̒���BD�ADC�ɒ��ڂ����
�@�@�@a�凙ABD�̖ʐρ�BD�~AD/2
�@�@�@b�凙ADC�̖ʐρ�DC�~AD/2
�@��ABD�Ƈ�ADC�͍���AD�������ł��邩��
�@�@�@a�Fb��BD�FDC
�ƂȂ�A��̎O�p�`�̏d���͂��ꂼ��̒�ӂ̒����ɔ�Ⴕ�Ă��邱�Ƃ�������B
������
�@�@�@BD��k�~a�ADC��k�~b
�ƂȂ���萔k��K���ɑI�Ԃ��Ƃ�
�@�@�@BD��a�ADC��b�ABC��a�{b
�Ƃ��Čv�Z���邱�Ƃ��ł���B
�������ƐԉH�̉�@���ł͊��m�̂��ƂƂ��ė��p����Ă���B
���w���ɂ��������@���̂P�@������
����n�߂ɁA��ABD�Ƈ�ADC�̒��BD��DC�ɁA�����œK���Ȓl�Ă͂߂Čv�Z���Ă݂�B
�}�P�ɂ����ā@BD�FDC��a�Fb�ł��邱�Ƃ���@a��6�Ab=3 ���������
�@�@�@BD�FDC��6�F3��2�F1
�ƂȂ�B
�����Œ����I��BD��12�ADC��6�ABC��18�Ƃ��Čv�Z����B
�@�@�@BE��BC/2��18/2��9
�@�@�@ED��BD�|BE��12�|9��3
��AED�Ƈ�GEF�͑����ł��邩��
�@�@�@AG�FGE��2�F1�AFD�FEF��2�F1
�@�]����
�@�@�@FD��ED�~2/3
�@ED��3���������
�@�@�@FD��3�~2/3��2
�@���@BF��BD�|FD��12�|2��10
�@�@�@FC��FD�{DC��2�{6��8
�͓_��B�A�x�_��C�A��p�_��F�Ƃ���ƁAB�ɂ������dFb��
�@�@�@Fb�~BC��W�~FC�@���@Fb��W�~FC/BC
�ƂȂ�B����� W��9�AFC��8�ABC��18 ���������
�@�@�@Fb��9�~8/18��4
���l�ɗ͓_��C�A�x�_��B�A��p�_��F�Ƃ���ƁAC�ɂ������dFc��
�@�@�@Fc�~BC��W�~BF�@���@Fc��W�~BF/BC��9�~10/18��5
�����Fb���b��4�іځAFc������5�іڂƂȂ�Z�z�́y���z�Ɠ����ɂȂ�B
���܂���œ����o��Ƃ�������B
���w���ɂ��������@���̂Q�@�ʁX��
����̎O�p�`��ʁX�ɍl����B
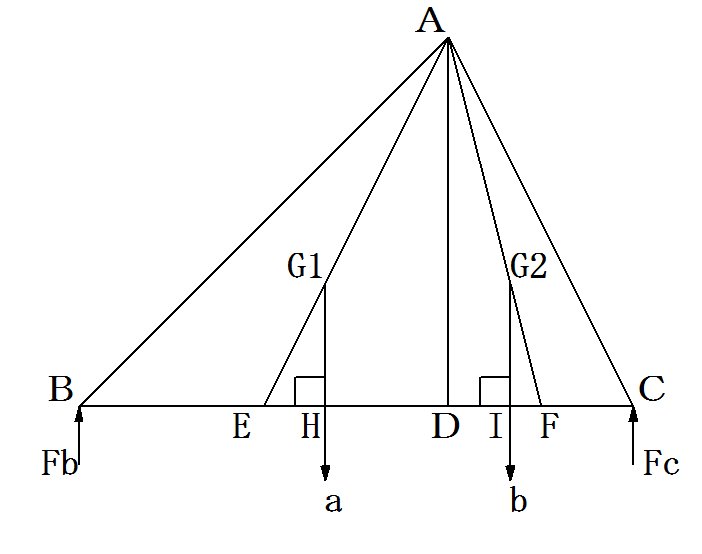 �}�Q�@��̎O�p�`�Əd�S
�}�Q�@��̎O�p�`�Əd�S
�@��ABD�̏d�������A��BD�̒��_��E�Ƃ��A��ABD�ɂ�����A��E������
�@�@�@AG1�FG1E���Q�F�P
�ƕ�������_��G1�Ƃ����G1�͇�ABD�̏d�S�ɂȂ�B
�@�d�SG1�����BD�ɉ��낵�������ƕ�BD�Ƃ̌�_�i�����̑��j��H�Ƃ���ƁA��ABD�̏d�����͓_H�ɍ�p����ƍl���邱�Ƃ��ł���B
�@��AED�Ƈ�G1EH�͑����ł��邩��
�@�@�@AG1�FG1E��2�F1�AHD�FEH��2�F1
�@�]����
�@�@�@HD��ED�~2/3=BD�~1/2�~2/3��BD�~1/3
�@�@�@BH��BD-HD=BD�~2/3
�@ �@HC��BD�~1/3�{DC
�@��ADC�̏d�������A��DC�̒��_��F�Ƃ��A��ADC�ɂ�����A��F������
�@�@�@AG2�FG2E���Q�F�P
�ƕ�������_��G2�Ƃ����G2�͇�ADC�̏d�S�ɂȂ�B
�@�d�SG2�����DC�ɉ��낵�������ƕ�DC�Ƃ̌�_�i�����̑��j��I�Ƃ���ƁA��ADC�̏d�����͓_I�ɍ�p����ƍl���邱�Ƃ��ł���B
�@��AFD�Ƈ�G2FI�͑����ł��邩��
�@�@�@AG2�FG2F��2�F1�ADI�FIF��2�F1
�@�]����
�@�@�@DI��DF�~2/3=DC�~1/2�~2/3��DC�~1/3
�@���ꂩ��
�@�@�@IC=DC-DI��DC�~2/3
�@�@�@BI��BD�{DI=BD�{DC�~2/3
�@�O�p�`�̔��x�����dFb��Fc�́A�x�_�Ɨ͓_��B��C�A��p�_��H��I��2�J���ɂ��邱�ƂŌv�Z�ł���B
�@�͓_��B�A�x�_��C�Ƃ����
�@�@�@Fb�~(BD+DC)��a�~HC�{b�~IC=a�~(BD�~1/3�{DC)+b�~DC�~2/3
�@�͓_��C�A�x�_��B�Ƃ����
�@�@�@Fc�~(BD+DC)=a�~BH�{b�~BI��a�~BD�~2/3�{b�~(BD+DC�~2/3)
�@������
�@�@�@BD��a�ADC��b�ABC��a�{b
�Ƃ����
�@�@�@Fb�~(a�{b)��a�~(a�~1/3�{b)�{b�~b�~2/3��1/3�~(a�{b){(a�{b)�{b}
�@�@�@���@Fb= 1/3�~{(a�{b)�{b}�@�E�E�E�@
�@�@�@Fc�~(a�{b)=a�~a�~2/3�{b�~(a�{b�~2/3)=1/3�~(a�{b){(a�{b)�{a}
�@�@�@���@Fc= 1/3�~{(a�{b)�{a}�@�E�E�E�A
�@�@�A�͎Z�z�́y�p�z�Ɠ����ł���B
�@�����a��6�Ab��3�Aa�{����9���������
�@�@�@Fb��1/3�~(9�{3)=4
�@�@�@Fc��1/3�~(9�{6)=5
�@�����Fb���b��4�іځAFc������5�іڂƂȂ�Z�z�́y���z�Ɠ����ɂȂ�B
���ʁX�ɍl���Ă����ʂ͓����ɂȂ�B
���w���ɂ��������@���̂R�@������ς���
���}�`�̖��͓K���ȕ⏕�����������Ƃʼn����̎����ɂȂ邱�Ƃ��ǂ�����B
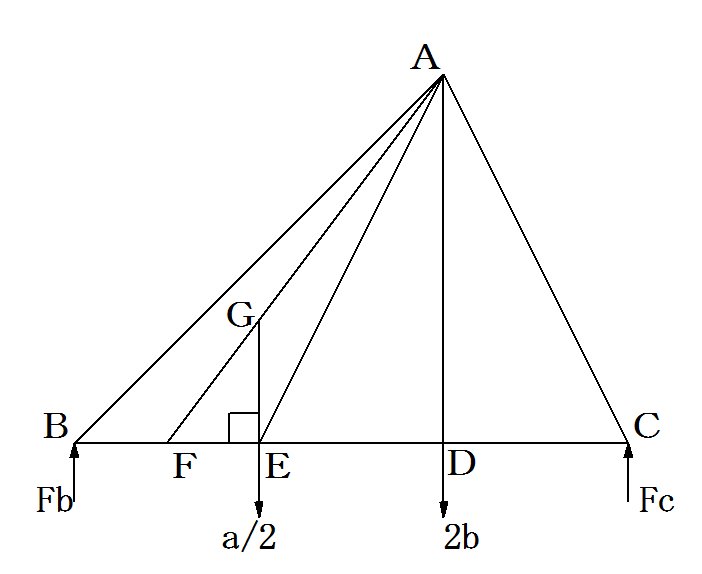 �}�R�@�Q�ӏ��̍�p�_
�}�R�@�Q�ӏ��̍�p�_
�@�}�R�ɂ����ā@��ABD�̕�BD�̒��_��E�Ƃ���ƁA
�@�@�@BE��ED��BD/2
�@�@�@BD�FDC��2�F1�@���@DC��BD/2
�@����������
�@�@�@BE��ED��DC
�ł���B
��ADC�Ƈ�ADE��AD�����Ƃ�����Ώۂ̒��p�O�p�`�Ŗʐς͓����ł��邱�Ƃ���A��AEC�̏d�S��AD��Ɉʒu���邽�߁A��AEC�̏d���i2b�j�͓_D�ɍ�p����ƍl���邱�Ƃ��ł���B
BE�̒��_��F�Ƃ��AE���琂���𗧂Ă�AF�Ƃ̌�_��G�Ƃ���B
�@�@�@BF��FE��BE/2��ED/2�@���@FE�FED��1�F2
�@�@�@��GFE�Ƈ�AFD�͑����@���@GF�FAG��1�F2
�@����������G�͇�ABE�̏d�S�ł���B
�@������
�@�@�@��ABE�̏d������ABD/2��a/2
�ł��邩��A��ABE�̏d���ia/2�j���_E�ɍ�p����ƍl���邱�Ƃ��ł���B
�O�p�`�̔��x����dFb��Fc�́A�x�_�Ɨ͓_��B��C�A��p�_��E��D��2�ӏ��ɂ��邱�ƂŌv�Z�ł���B
������ BE��ED��DC��L �Ƃ��A�͓_��B�A�x�_��C�Ƃ����
�@�@�@Fb�~3L��a/2�~2L�{2b�~L�@���@Fb���ia�{2b�j/3
�@�����a��6�Ab��3���������
�@�@�@Fb���i6�{2�~3�j/3��4
���l�ɗ͓_��C�A�x�_��B�Ƃ����
�@�@�@Fc�~3L��a/2�~L�{2b�~2L�@���@Fc���ia/2�{4b�j/3���i6/2�{4�~3�j/3��5
����čb��4�іځA����5�іڂƂȂ�Z�z�́y���z�Ɠ����ɂȂ�B
�����̉�@�͍��E�̎O�p�`�̏d���̔䗦���Q�F�P�̂Ƃ������̓��ꎖ��B
�����@����₷���⑫
�������̌����@�̂Ȃ��ŁA���w���ł͂�����ƕ�����ɂ������ȕ����ɐ�����������B
 �}�P
�}�P
�@�}�P�ɂ�����
�@�@�@BF��BD�|FD
�@�@�@�@��AED�䇙GEF�@���@AG�FGE���Q�F�P�ADF�FFE���Q�F�P
�@�@�@�@��FD��2/3�~DE
�@�@�@�@�@DE��BD�|BE��BD�|((BD�{DC))/2��((BD-DC))/2
�@�@�@�@�@FD= 2/3�~�o1/2�~(BD-DC) �p��1/3�~(BD-DC)
�@�@�@�@��BF��BD- 1/3�~(BD-DC)��1/3�~(2BD�{DC)��1/3�~(2a�{b)
�@�@�@�@�@FC��FD�{DC��1/3�~(BD-DC)�{DC��1/3�~(BD�{2DC)��1/3�~(a�{2b)
�@��ABC�̏d��W��a�{b�ł��邩��A�x�_��C�A��p�_��F�A�͓_B�ɂ������d��Fb�Ƃ����
�@�@�@�@W�~FC��Fb�~BC
�@�@�@�@��Fb��(W�~FC)/BC��1/(a�{b)�~(a�{b)�~(a�{2b)/3��1/3�~(a�{2b)��1/3�~�iW�{b�j�E�E�E�@
�@�x�_��B�A��p�_��F�A�͓_C�ɂ������d��Fc�Ƃ����
�@�@�@�@W�~BF��Fc�~BC
�@�@�@�@��Fc��(W�~BF)/BC��1/(a�{b)�~(a�{b)�~(2a�{b)/3��1/3�~(2a�{b)��1/3�~(W+a)�E�E�E�A
�@�@�A�͎Z�z�́y�p�z�Ɠ����ł���B
�@������W���X�Aa���U�Ab���R���������
�@�@�@Fb���S�AFc���T
�@�b���S�іځA�����T�іڂƂȂ�Z�z�́y���z�Ɠ����ł���B
���Z�z�́y�p�z�́A���E�̎O�p�`�̏d���̔䗦���ݖ�ƈقȂ�ꍇ�ł��e�Ղɓ����������ʉ��ł���B
�@�@�@��j�@���F9�A�E�F3�̏ꍇ�@���@�b�F5�A���F7
�@�@�@�@�@�@���F12�A�E�F3�̏ꍇ�@���@�b�F6�A���F9�@�Ȃ�
���Z�̐��w���x��
�����܂ł͒��w�Z�̐��w�Ɨ��Ȃʼn����郌�x���ł������A���Z�̐��w�ŏK���u�d�S�Ɋ֘A��������v�𗘗p����Əd�S�̈ʒu������Ȃ蓾���Ă��܂��܂��B
�����_�̍��W�����߂��������
�������_�̕�����������d�S�̈ʒu�����Ƃ��ł���B
 �}�P
�}�P
�@�}�P�ɂ����āA����ED�ɂ�����_E�AD�̍��W��E(e)�AD(d)�Ƃ��AED�����F���ɓ�������_F�̍��W��F(f)�Ƃ���Ƃ��A
�@�@f���i���~e�{���~d�j/�i���{���j
�Ƃ��������_�̕�������������B
������e��(a�{b)/2�Ad��b�A����1�A����2�Ƃ����
�@�@f���o2�~�ia�{b�j/2�{1�~a�j�p/�i1�{2�j���i2a�{b�j/3
�ƂȂ�B
�]����
�@�@BF���i2a�{b�j/3�E�E�E�@
�@�@FC��BC�|BF���ia�{b�j�|�i2a�{b�j/3���ia�{2b�j/3�E�E�E�A
���ꂩ��
�@�@�@�@�@Fb��(W�~FC)/BC
�@�@�@�@�@Fc��(W�~BF)/BC
�@������
�@�@�@W��a+b�ABC��a+b�Aa��6�Ab��3�Ƃ����
�@�@�@Fb��1/3�~(a�{2b)��1/3�~(6�{6)=4
�@�@�@Fc��1/3�~(2a�{b)��1/3�~(12�{3)=5
�@�����Fb���b��4�іځAFc������5�іڂƂȂ�Z�z�́y���z�Ɠ����ɂȂ�B
�d�S�̍��W�̌�������
���O�p�`�̏d�S���W�̌��������p���ē������Ƃ��ł���B
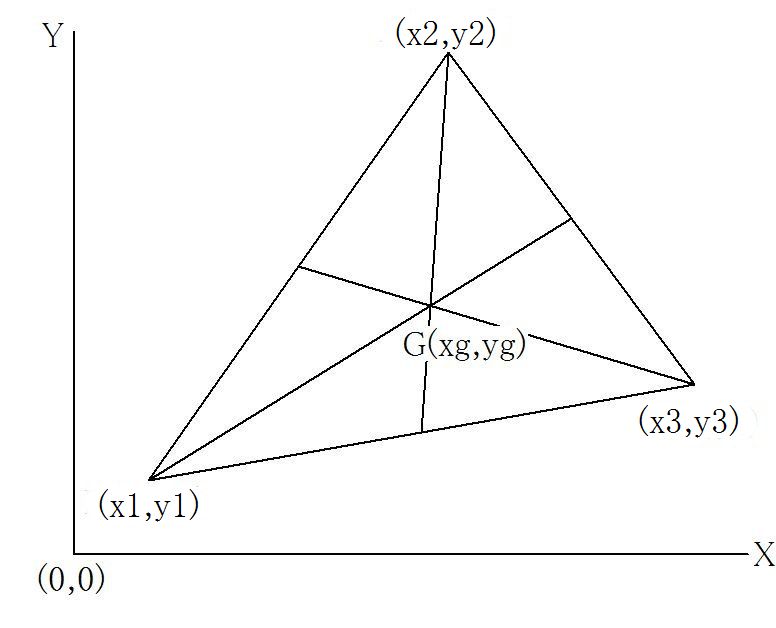 �@�O�p�`�̒��_�����W�ixi,yi�j�ŕ\���Ƃ��A�d�S�̍��W�ixg,yg�j��\��
�@�O�p�`�̒��_�����W�ixi,yi�j�ŕ\���Ƃ��A�d�S�̍��W�ixg,yg�j��\��
�@�@�@xg���ix1�{x2�{x3�j/3
�@�@�@yg���iy1�{y2�{y2�j/3
�Ƃ�������������B
�}�S�@�d�S�̍��W
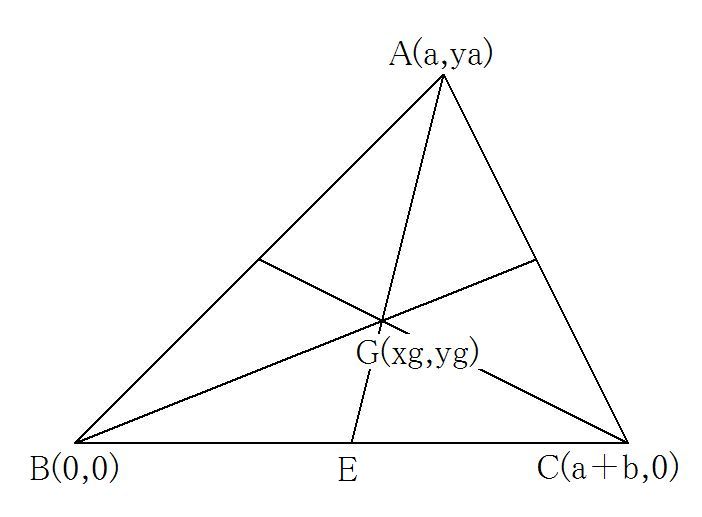 �@�ݖ�ɉ����ĎO�p�`�̒��_�̍��W��}�S�̂悤�ɂ���B
�@�ݖ�ɉ����ĎO�p�`�̒��_�̍��W��}�S�̂悤�ɂ���B
�@�@A�ia,ya�j�AB�i0,0�j�AC�ia+b,0�j
�}�T�@�ݖ�̏d�S���W
���̂Ƃ�
�@�@�@xg���oa�{0�{�ia�{b�j�p/3���i2a�{���j/3
�ƂȂ�B
���ꂩ��}�P�ɂ�����
�@�@�@BF��xg��(2a�{b)/3
�@�@�@FC��BC�|BF��(a�{2b)/3
�ƂȂ�A�O���Ɠ��l�ɂ���Fb�AFc�����߂邱�Ƃ��ł���B
�p���[�X�|�b�g
���R���w�蕶�����u�R�c����̖�t���v
 ��t��
��t��
��t���́A����11�N�i1828�N�j�̏㓏�ŊԌ�15�ډ��s��15�ڂ̌����B���ɕ��d���R�ڒ��o���Ă���B�����͒���s�����̐����^�쐶�ۂŁA�������͋v�ۂ̐��ܘY���q�ł���A�}�ʂ��������B
�@�`���I�ɂ͕��O�ԓ��̂悤�ɍ��ꂽ���ꉮ����A�����̌����Ő��ʂɈ�Ԃ̌��q��t���Ă���B���͓�ԂŐ�Ƃ���B
�@�����͌��q�̖ؕ@���U�����̓����q�A�g����ɗ��A�g���̊G�l�ɔg�E�T�A�苷�݂ɋe���Ē���Ƃ���B�܂��A�����̖ؕ@�́A���E�߂��Ē���Ƃ���ȂNjZ�I�I�Ȓ����𑽂����Ă���B
 ��t������
��t������
�����ɂ͌��E���݂����Ă��邪�A�T���V�`�W���A10���V�`�W���̂��Ղ�ɂ͌��E���͂����āA��������̂̋�ԂƂȂ�B
�@��t�@����{���Ƃ����E�ɓ�����F�A������F���]���Ă���B
�y���R���w�蕶�����z�y���쌧�����Z�z�W�听�@�Z�z�ւ̏��ҁz�w��R�j�k�x���
�@�p���[�X�|�b�g
�������i���E�{��s�����j�̘a�Z�ƁE���c���S���B���y�p�z���o�������@�́A�����@�̂悤�ɂ��ĒH�蒅�������A����Ƃ��d�S�Ɋւ��������m���Ă����̂��A���邢�͂����Ƃ͂܂������قȂ�a�Z�Ɠ��̌����𗘗p�����̂��s���ł����A��������Ɛ������y�p�z�̋L�q�͑f�l�ڂɂ��Ȍ����Ăł������ł��B
�@������������Ƃɐ��������Ƃ��͕G���ۂ�ƒ@���Ăɂ�܂肵�����A�������̂��܂��яオ���Ė��������A�͂��܂�����肵�Ċ�сA���̊������w�Z�z�x�ɂ��Ė�t���ɕ�[�����̂ł͂Ȃ����ȂǂƑz�����Ă��܂��܂��B
�R�c�����t���́w�Z�z�x�̖������㐔�w�ʼn����������M�펁�ƐԉH��ߎ��͒��쌧�ɂ�����a�Z�����̑��l�҂ŁA�u����v�Ɓu�����@�v�̈��p�������肢�����Ƃ���A�������������������܂����B��������\���グ�܂��B
�@��������̒����ɂ��ƒ��쌧���ɂ͂V�S�ʂ̎Z�z���������Ă���A�R�c�����t���̎Z�z�͂��̂�����1�ʂŁA���̋M�d�ȕ������Ƃ�����ł��傤�B
�R�c����̖�t�����w�Z�z�x�̗쌱�ɂ���Ċw�ƁA���ɐ��w�E���Ȃ̗���͂����܂�p���[�X�|�b�g�Ƃ������Ƃɂ���A�V���������ɂȂ邩����������܂���B
![�����M�펁�]��](sangaku/nakamuranobuya20190409.jpg) �@2019�N�i����31�N�j4��9���̐M�Z�����V���ɒ����M�펁�̐��������Ă��܂����B
�@2019�N�i����31�N�j4��9���̐M�Z�����V���ɒ����M�펁�̐��������Ă��܂����B
�@���̃y�[�W���܂Ƃ߂�ɂ�����A�����Ȃ�d�b�ň��p���̂��肢�������ۂ́A�����ɉ������������Ƃɉ��߂Ċ��Ӑ\���グ�܂��B
�@���̂Ƃ����R���w�Z�Ζ����ɖ�t���̎Z�z�����ꂽ���b��A�v�ۂ̘a�Z�ƁE���R�`���ɂ��Ă̘b��Ȃǂ����������v���o����܂��B
�@�ނ�ł�����ݐ\���グ�܂��B
�Q�l�ɂ����Ă�������������
- �ԉH��߁w�M�Z�̘a�Z�x�M�Z�����o�ŕ��A���a53�N
- ���R���u�R�c����̖�t���ɂ��āv�w��R�j�k�xNo.12�A���R�x�k��A����27�N10��
- �k���M�u�{��̘a�Z�� �y���C�����e�v�w�{���xNo.52�A�{�����y�j������A2001�N4��
- �{��s�y�L����2017.10�i����29�N�j�z
- �M���������ƍ��c�@�y�M���ܑ�18���ҁi����23�N�x�j�z
- �w�M�B���R�����x����j�ҁA���R�������s��A����17�N
- �w�M�B���R�����x��O���n���ҁA���R�������s��A����18�N
- ���쌧���R���@�y���R���w�蕶�����z
- �����M��w�]�ˎ���̎Z�p�@�w�c���o���L�x�x����9�N�A���珑��
- �����M��@�y���� ���Ⓑ�쌧�̎Z�z�z
- �����M��@�y���y�̎Z�z : ���k�M�n���z1964�N�A��������}���كT�[�`
- �����M��@�y���쌧�����Z�z�W�听�@�Z�z�ւ̏��ҁz
- �����M��ق��w�G�n�Z�z�ւ̏��� : ���㐔�w�ɂ���@ : ���쌧�����Z�z�W�听�x����11�N�A���珑��
- �����M��ق��@�y���쌧���Z�z�W�听�@���̎Z�z�@�\���㐔�w�ɂ���@�\�z
- �a�Z�̊ف@�y��t���iYakushido Temple�j�z
�ŏI�X�V�@2019�N 4��10��